The following cipher is designed with use in the field in mind. Whenever a letter must be converted to a number the fairly standard conversion a=1, b=2, ..., z=26 is used. Performing an encryption consists of 2 parts
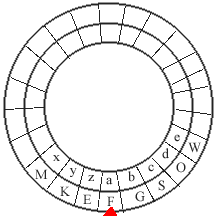
Two keys are used in this algorithm. The first is a general mono-alphabetic substitution i.e. a mapping from the 26 plain text letters to 26 cipher letters. This would generally be built into a small device given to those doing encryption. The device would consist of a wheel with the substitution written on it. The wheel could rotate and would have a small pointer to a specific letter. Thus it would look something like:

Of course a real key would have 26 letters and be completely filled in. The two alphabetic rings would rotate together but the red arrow would not rotate with them. This key would not be changed very often.
The second key would be a keyword or phrase which was changed frequently
In order to do an encryption one should obviously have the text to be encrypted along with a mono-alphabetic key and plain keyword. For our example we will use:
| A short little example |
| Plain letter: | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cipher Letter: | X | K | U | S | R | T | I | J | V | A | Z | F | C | Y | W | P | B | H | N | L | G | E | D | O | M | Q |
| cat |
Once you have the above information you can begin. First write down the numerical equivalent of the keyword for easy use later
| cat | = | 3, 1, 20 |
Also write down the reversed numerical keyword (be sure to keep them straight).
| tac | = | 20, 1, 3 |
Finally have a piece of graph paper handy and mark out exactly enough space for the number of letters in your message plus one more space. Also leave a row of blocks beneath this space. Our example has 19 letters so we need 20 spaces. (remember don't count spaces and other non-letters).
Finally, prefix your message with a single random character. This character could be obtained by spinning your disk and seeing what letter the mark landed on. Now you are ready to begin encrypting.
| g a short little example |
The first step is to carry out the stream enciphering. As you do, the message should be written onto your graph paper for ease of the next step.
The stream cipher uses the mono-alphabetic key described above along with the numeric key created above. There are two ways to view the stream cipher. One is more mechanical in nature the second more mathematical. We will cover the mechanical one first.
Using the cipher wheel described above one would begin by setting the red arrow to the plain-text letter 'a' (the position picture above). To encrypt a letter the following steps would be performed).
Each subsequent letter would be encrypted in the same way but with the wheel in the state created by encrypting the last letter. One thing which was ambiguous about the above directions was the use of the current number in the numeric key
. For the first letter encrypted use the first number of the numeric key, for the second letter encrypted use the second number of the key and so on. When you run out of numbers in the numeric key go back to the first number.
An alternate explanation of the above process is as a math computation using mods. Keep a variable state which will start with the value 1. To encrypt a letter l when k is the current number of the numeric key simply calculate (state+l+k) mod 26. This value becomes the new value of state. To get the cipher letter, take this value, turn it into a letter and apply the mono-alphabetic substitution.
In our example the first letter is 'g' and the first number in the numeric key is 3. Remember the state starts at 1, so we compute 1+'g'+3 mod 26 = 'k'. Then applying the mono-alphabetic substitution we see this encrypts to 'Z'. To encrypt the second letter which is 'a' we compute 'k'+'a'+1 mod 26 = 'm' and this becomes the new value of state. The cipher letter is then 'C' because this is what the mono-alphabetic substitution sends 'm' to. Completing this on the rest of our message we have:
| Z | C | Q | Z | X | C | A | D | Q | D | H | O | T | F | S | J | E | T | G | X |
Once the stream encryption has been performed you must perform the keyed decimation. This step will use the reversed numeric key and the graph paper describe in the setup above.
| tac | = | 20, 1, 3 |
Use the reversed numerical keyword. Start before the first letter:
| Z | C | Q | Z | X | C | A | D | Q | D | H | O | T | F | S | J | E | T | G | X | |
| ^ |
Skip the number of unchosen letters indicated by the keyword's first number (in this case 20). If you run off the end simply go back to the beginning. In this case it brings us to 'Z' because there are 20 letters in our example. Number this letter as 1 (the first letter chosen).
| Z | C | Q | Z | X | C | A | D | Q | D | H | O | T | F | S | J | E | T | G | X | |
| 1 | ^ |
Now, skip the number of unchosen letters indicated by the keywords next number, and number this character as the next chosen character. In this case skip 1 and chose 'Q' mark this as 2.
| Z | C | Q | Z | X | C | A | D | Q | D | H | O | T | F | S | J | E | T | G | X | |
| 1 | 2 | ^ |
Repeat the above step using the next number in the key (when the end of the key is reached loop back to the beginning) until all letters have been chosen.
| Z | C | Q | Z | X | C | A | D | Q | D | H | O | T | F | S | J | E | T | G | X |
| 1 | 12 | 2 | 18 | 19 | 7 | 3 | 15 | 8 | 16 | 4 | 10 | 5 | 13 | 9 | 11 | 6 | 20 | 14 | 17 |
Now read off the letters in the order given by the numbers.
| Z | Q | A | H | T | E | C | Q | S | O | J | C | F | G | D | D | X | Z | X | T |
This gives the encrypted text, ready to send.
To decrypt prepare the keys in the same manner. First undo the keyed decimation. This can be done using graph paper. Skip blank spaces as dictated by the key and place letters from the encrypted message down in the places they would have been pulled from. Then undo the stream cipher. This can be done by subtracting rather than adding, just make sure to set the state correctly. If more decryption info is needed simply email us. Decryption does work, the above example was successfully decrypted with our encrypt/decrypt code.
This cipher is not exactly the cipher we had intended to publish. This is however, the cipher that ended up being used for our third cipher and so that is what we published. This method requires the message be written out in its entirety between the stream and keyed decimation steps. If instead of the above method one first does the stream cipher then the keyed decimation decryption, this can be done without writing down any intermediate steps. The keyed decimation encrypt/decrypt are simple inverses and it is not stronger to use one or the other, thus they can be switched. That is the cipher we had originally intended to publish because it would have been slightly simpler to do an encryption in the field without leaving dangerous evidence behind.
 |
jwalker@cs.oberlin.edu |