CSCI 151 - Lab 8 Priority Queues

This is due on Wednesday, May 11

Priority queues are useful for finding and removing the largest or smallest value from a collection of data. If you have a collection of data and want to find the k largest values or the k smallest values in the collection without taking the time to sort the whole collection, priority queues are the way to go.

The zipped folder Lab8.zip contains a template for your MyPriorityQueue class, and files Scheduler.java and Task.java for an application that you will complete. It also contains files for 5 Task comparators. Unzip this folder, change the name of tthe Lab 8 folder to Lab 8 <Your Name> and install it as your lab8 project folder before you go into Eclipse to start the Java project for this lab.

A Reminder About Comparators

The Comparator<T> interface just says that a class contains a method

	int compare(T x, T y)

This function is used to determine the ordering of elements x and y: if compare(x, y) < 0 then x comes before y in the ordering used for the priority queue; if compare(x, y) > 0 then x comes after y. By interchanging the positive and negative values that the comparator returns we can change the prioroity queue from giving us the smallest values in its colllection to giving us the largest values.

Because we might want to change comparators, priority queues don't expect comparison methods to be built into a class. Rather, we will make a standalone class that implements the Comparator<T> interface, and give an object of this class to our priority queue constructor.

For example, suppose we have a Person class with a method age( ) that gives a person's current age and we want to be able to find the youngest persons. Here is a comparator class that will do this:

     class OrderFromYoungest implements Comparator<Person> {

         int compare(Person x, Person y) {
                if (x.age() < y.age())
                      return -1;
                else if (x.age() == y.age())
                      return 0;
                else return 1;
        }
    }
On the other hand, if we want the queue to find the oldest persons we might use the comparator 
     class OrderFromOldest implements Comparator<Person> {

         int compare(Person x, Person y) {
                if (x.age() < y.age())
                      return 1;
                else if (x.age() == y.age())
                      return 0;
                else return -1;
        }
    }
In either case we can use a Comparator object to construct a priority queue, as in 
MyPriorityQueue PQ = new MyPriorityQueue( new OrderFromYoungest() );

Part 1 - Concepts

We will use binary heaps to implement priority queues. A heap is a tree in which every node has a value that is less than or equal to the values of its children. Furthermore, we will use trees that are complete, meaning that they have every possible node at each level above the bottom row of leaves, amd that will have every possible node from left to right until the nodes of the tree are exhausted.

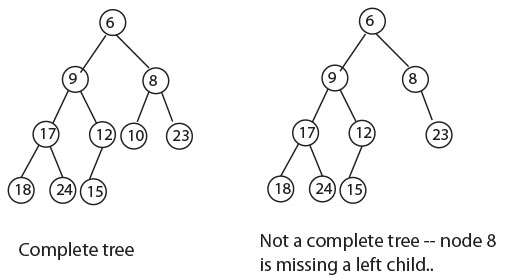
Because we use complete trees we can store them in an array or ArrayList of base-type T. When doing this it is traditional, though not absolutely necessary, to skip entry [0] and put the root of the tree at index [1]. Here, for example, is the array representation of the complete tree shown above at the left:

The two children of the root are at indices [2] and [3]; the children of the root's left child are at indices [4] and [5], and so forth. In general the two children of the node at index n are at [2*n] and [2*n+1]. On the other hand, the parent of the node at index [n] is at index [n/2] where this division does integer arithmetic: 7/2 is 3, not 3.5.

If we want to add a new value to the priority queue we do so at the only available spot: the next unused entry in the array, which corresponds to the next available leaf in the tree. Note that if the queue currently has size N, then its nodes are at indexes [1] through [N], so the next available slot in the array is at index [N+1]. After adding the value to the array we go through a process called "percolating up". We compare the value to the value at its parent node; if the value is less than the parent (violating the heap property), we switch it with its parent and then recurse on the parent's index. This process stops either when the inserted value is greater than or equal to its parents value (thus restoring th.e heap property) or when the inserted value has moved up to the root, i.e. index [1].

The smallest value in the heap is always at the root: index [1]. If we want to "poll" or remove and return this minimum value, we save it somewhere (you can make a temporary variable or use [0] of the array) then put the last leaf of the tree into the root (remember that if the queue has N values then the last leaf is at index [N]; we move this value to index [1] and reduce the size of the queue). Now we go through a process called "percolating down". We compare the newly moved value to the values of its two children; if it is larger than either we switch it with the smaller child and recurse on the child's index. This continues until the value is smaller than both its children if it has 2, or its only child if it has just one, or until it has no children. After this "percolating" process has ended we return the value of the old root that we saved at the start of this process.

Note that though we usually think of a heap as living in an array, we will actually implement it in an ArrayList to avoid resizing issues. Note that the size of the heap is different from the size of the ArrayList. For a heap of size N the underlying ArrayList must have size at least N+1. I suggest maintaining your own size variable.

Part 2 -- Priority Queue Methods

You need to implement class MyPriorityQueue<T>. We will base the queue on an ArrayList<T>. Here are the methods you need to implement:

Constructor: public MyPriorityQueue<int initial_capacity, Comparator<T> comp);

The constructor should construct the ArrayList (give the ArrayList constructor the initial_capacity), and add null to it to occupy the empty [0] slot. It should save the comparator in an instance variable; all comparisons in the queue use comp.compare rather than < or >. It should also initialize any other variables you plan to use, such as a counter for the size of the queue.

public int size();

Your queue has a different size than the underlying ArrayList, so you should maintain your own private size variable. This method just returns it.

private int parent(int myIndex);
private int leftChild(int myIndex);
private int rightChild(int myIndex);

These three methods give the indices of the parent and children of a node in terms of the node's index.

private void percolateUp(int index);

This compares the data at index with the data in its parent node. If the parent value is larger the two nodes swap their values, then recurse on the parent's index..

private void percolateDown(int index);

This compares the data at index with the data in its children. If the value at index is not less than or equal to that of its kids swap it with its smaller child and recurse on the child's index. This is the only tricky piece of coding in this lab. At each step there are three cases to consider: a node might have no children (2 * its index is more than the size of the queue), it might have exactly one child (2 * its index is exactly the size of the queue) or it might have 2 children.

public T peek();

This returns the smallest value in the queue, or null if the queue is empty. Of course, if the queue is not empty the smalllest value is always at the root, index [1].

public T poll();

This removes and returns the smallest value in the queue: Save the value at index [1] somewhere, move the value of the last child into index [1], reduce the size by 1, then call percolateDown(1). Finally, return the old root that you saved. Of course, if the queue is empty don't do any of this; just return null.

public boolean offer(T value);

This adds the new value to the queue and returns a boolean that says whether or not the addition happened. There is no limit to the size of an ArrayList, so your method should always return true. If the queue currently has size N, do the addition by adding the data to the ArrayList at index [N+1], then call percolateUp(N+1). Don't forget to increment your size to N+1 to reflect the addition.

Testing: It is hard to do much testing until you have an at least partially working heap. I suggest writing size(), percolateUp( ), offer( ), and peek() in one go before you start testing. The percolate methods are the only likely sources of bugs. Once you have the methods needed for insertion, start an empty queue, offer it some values, and use peek( ) to determine whether the smallest value is indeed at the root, as it should be. Once you have the insertion methods running correctly, add the two remaining methods percolateDown( ) and poll(). One way to test the complete system is to offer a sequence of values to a queue, then poll it in a loop until the queue is empty, printing the result of each poll(). That should print the values you inserted in order from smallest to largest.

Part 3 – Process scheduling

Priority queues are commonly used to schedule tasks in real time: as a task becomes available, you add it to the priority queue, and then when you have resources available, you run the task at the top of the queue. We are going to use your priority queue to simulate an operating system scheduler picking which program to run on your CPU - however, this same algorithm is also used to schedule things like which patients to attend to in an Emergency Room.

For this simulation you need two Java classes: Task.java and Scheduler.java, and a variety of comparators.  Task represents the programs you are scheduling, Scheduler represents your OS scheduler, and AvailableComparator is an example of a Comparator

As you can see by looking at Task.java, Task is an extremely simple class that just holds information about tasks to be scheduled. Every task has a name, a priority, an earliest available time, a time length and a deadline. The lab includes three text files representing lists of tasks: jobs10.txt, jobs100.txt and jobs1000.txt.

You will be implementing a variety of OS scheduling algorithms by various comparators that compare two tasks on each of these variables. We have already implemented AvailableComparator.java, which sorts jobs by the time at which they become available to be scheduled; this is equivalent to the First Come First Serve scheduling algorithm. You will implement the following:

Once you have implemented a Comparator, you will be able to test it out using the Scheduler class, which simulates an OS scheduler. Scheduler takes two command line arguments: a text file of jobs, and a string indicating which comparator to run. The strings it expects are "available", "deadline", "length", "name", and "priority".

It is late in the semester. If your primary concern is just to be done with this lab your only task for this part is to complete the four named comparators (the files we give you have stubs for them). You can test your implementations by comparing the output of the scheduler program with what we give below. Of course, no one wants to admit only wanting to be done, so here is a description of how the Scheduler program works.

The first step is to read the jobs file. Each line has the information needed to construct a Task, The program does so and offers the task to a MyPriorityQueue<Task> queue called tasks which is ordered by the availableTime value. The head of this queue always has the smallest availableTime.

The scheduler starts a second MyPriorityQueue<Task> queue called runOrder which is organized by the comparator you choose in the RunConfiguration arguments and then enters a long loop where it checks in on the state of the world every 10 milliseconds. At each step it

  1. Removes from tasks and offers to runOrder any task whose availableTime is prior to the current time step.
  2. Looks to see if the currently running task (if there is one) has completed. If so it stops the task.
  3. If there is now nothing currently running it polls the runOrder queue to find the next task to run and begins to run it.

The simulation also keeps track of missed deadlines and priority inversions. Deadlines are easy. Every task has a deadline; if a task completes after its deadline a deadline counter is incremented, This counter is printed after all tasks have been completed. Inversions need a little more thought. An inversion occurs when a task completes prior to other tasks in the runOrder queue that have higher priority. Our priorities are numbers betweeen 0 and 9. We maintain an array of 10 integer counters that say how many tasks currently in the runOrder queue have a given priority. This is incremented when a task enters the queue and decremented when the task completes. When we finish a task with priority 6, the counts in this array for priorities 7, 8, and 9 are summed; our task had this many inversions. At the end of its run our scheduler prints the total number of inversions. Naturally, we would like that to be as small as possible, though we can't eliminate all priority inversions.

The results of running a variety of scheduling algorithms on jobs10.txt are below. The number before the colon is the current timestep.

Scheduling jobs by Length

 0: running terry-furor priority 4 availability 0 length 48 deadline 140 0 other jobs in queue.  
50: running ample-roads priority 1 availability 38 length 40 deadline 192 0 other jobs in queue.  
90: running mixes-tones priority 8 availability 53 length 33 deadline 135 0 other jobs in queue.  
130: running fetch-strum priority 2 availability 130 length 75 deadline 318 1 other jobs in queue.  
210: running snare-ideal priority 8 availability 192 length 18 deadline 358 3 other jobs in queue.  
230: running roses-octet priority 5 availability 141 length 52 deadline 365 2 other jobs in queue.  
290: running mural-savor priority 4 availability 250 length 36 deadline 313 3 other jobs in queue.  
330: running aging-sated priority 2 availability 239 length 75 deadline 436 2 other jobs in queue.  
410: running crude-maybe priority 9 availability 172 length 78 deadline 345 1 other jobs in queue.  
490: running samba-inked priority 4 availability 100 length 87 deadline 296 0 other jobs in queue.  
All jobs have been run. 
3 deadlines were missed, by a total of 437 milliseconds. 
There were 5 priority inversions.

Scheduling jobs by Deadline

 0: running terry-furor priority 4 availability 0 length 48 deadline 140 0 other jobs in queue.  
50: running ample-roads priority 1 availability 38 length 40 deadline 192 0 other jobs in queue.  
90: running mixes-tones priority 8 availability 53 length 33 deadline 135 0 other jobs in queue.  
130: running samba-inked priority 4 availability 100 length 87 deadline 296 1 other jobs in queue.  
220: running fetch-strum priority 2 availability 130 length 75 deadline 318 3 other jobs in queue.  
300: running mural-savor priority 4 availability 250 length 36 deadline 313 4 other jobs in queue.  
340: running crude-maybe priority 9 availability 172 length 78 deadline 345 3 other jobs in queue.  
420: running snare-ideal priority 8 availability 192 length 18 deadline 358 2 other jobs in queue.  
440: running roses-octet priority 5 availability 141 length 52 deadline 365 1 other jobs in queue.  
500: running aging-sated priority 2 availability 239 length 75 deadline 436 0 other jobs in queue.  
All jobs have been run. 
5 deadlines were missed, by a total of 462 milliseconds. 
There were 2 priority inversions.

Scheduling jobs by Priority

 0: running terry-furor priority 4 availability 0 length 48 deadline 140 0 other jobs in queue.  
50: running ample-roads priority 1 availability 38 length 40 deadline 192 0 other jobs in queue.  
90: running mixes-tones priority 8 availability 53 length 33 deadline 135 0 other jobs in queue.  
130: running samba-inked priority 4 availability 100 length 87 deadline 296 1 other jobs in queue.  
220: running crude-maybe priority 9 availability 172 length 78 deadline 345 3 other jobs in queue.  
300: running snare-ideal priority 8 availability 192 length 18 deadline 358 4 other jobs in queue.  
320: running roses-octet priority 5 availability 141 length 52 deadline 365 3 other jobs in queue.  
380: running mural-savor priority 4 availability 250 length 36 deadline 313 2 other jobs in queue.  
420: running fetch-strum priority 2 availability 130 length 75 deadline 318 1 other jobs in queue.  
500: running aging-sated priority 2 availability 239 length 75 deadline 436 0 other jobs in queue.  
All jobs have been run. 
4 deadlines were missed, by a total of 426 milliseconds. 
There were 0 priority inversions.

 

handin

Look through your .java files and make sure you've included your name and the name of anyone you worked with at the top of all of them.

Include in your submission a file named README. The contents of the README file should include the following:

  1. Your name and your partner's name if you worked with someone
  2. A statement of the Honor Pledge
  3. Any known problems with your classes or program

As usual, make a zipped copy of you project folder (which should be Lab8<your last name>) and hand it in on Blackbard as Lab7.