Parsing and Unparsing

Chapter: Parsing and Unparsing

Whenever an interpreter interprets a given piece of input, two things need to happen. First, the input needs to be parsed, or separated out, into its component parts in such a way that the parts can be easily worked with. Then the interpreter can go about its job of interpreting. The parsing deals with the syntactic considerations, and the interpreting deals with the semantic considerations.

Q. 3

Why do we need to separate out these two steps? Can't we just combine them together?

The actual syntax of a language like Scheme is known as a concrete syntax. The syntax generated by a parser and used by an interpreter is known as an abstract syntax. Before we generate a parser, then, we need to decide on an abstract syntax, and how it will be represented. We will work with whose concrete syntax is defined by the grammar below.

<exp> ::= <number>		
        | <id>		  
        | (lambda (<id>) <body>)  
        | (<exp> <exp>)

This grammar can work with numbers, variable references, lambda expressions of one variable, and applications of one expression to another.

In order to make an abstract syntax for this grammar, we need to decide on a name for each production in the grammar, and names for each nonterminal in the production. One possible choice is


<exp> ::= <number>		  lit-exp (datum)
        | <id>			  var-exp (id)
        | (lambda (<id>) <body>)  lambda-exp (id body)
        | (<exp> <exp>)		  app-exp (rator rand)

(In this example, rator stands for operator and rand stands for operand.)

It is easiest to reason about an abstract syntax representation as an abstract syntax tree. As an example, the abstract syntax tree for the expression ((lambda (x) (f x)) 3), following the specification above, looks like this.

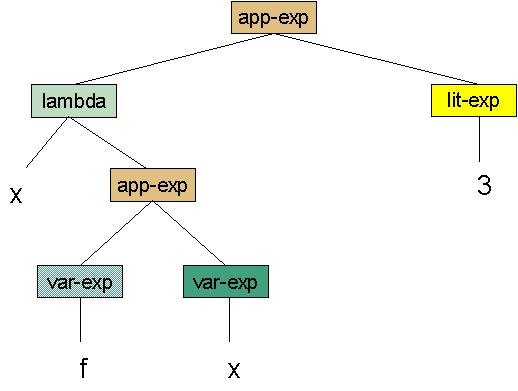
We will use the define-datatype mechanism described in EOPL, and provided by Dr. Scheme. In order to use define-datatype you must have (require (lib "eopl.ss" "eopl")) at the top of your file.

With define-datatype we define each production to be a variant of the datatype expression. Each variant has fields corresponding to the names of the nonterminals. Here is the definition we will use. It is almost identical to the code in section 2.2 of EOPL.

(define-datatype expression expression? 
  (lit-exp 
   (datum number?))
  (var-exp
   (id symbol?))
  (lambda-exp
   (id symbol?)
   (body expression?))
  (app-exp
   (rator expression?)
   (rand expression?)))

Given this definition, a parser can be defined very easily.

(define parse-expression
  (lambda (datum)
    (cond
      ((number? datum) (lit-exp datum))
      ((symbol? datum) (var-exp datum))
      ((pair? datum)
       (if (eqv? (car datum) 'lambda)
           (lambda-exp (caadr datum)
                       (parse-expression (caddr datum)))
           (app-exp
            (parse-expression (car datum))
            (parse-expression (cadr datum)))))
      (else (error 'parse-expression
             	   "Invalid concrete syntax ~s" datum)))))

It is sometimes useful to be able to unparse something represented in abstract syntax. It is equally easy to write unparse in Scheme:

(define unparse-expression
  (lambda (exp)
    (cases expression exp
           (lit-exp (datum) datum)
           (var-exp (id) id)
           (lambda-exp (id body) 
                       (list 'lambda (list id)
                             (unparse-expression body)))
           (app-exp (rator rand)
                    (list (unparse-expression rator)
                          (unparse-expression rand))))))

Unfortunately, when you use define-datatype to build your data structures, the details of the underlying component structure are not revealed. You can peek at that component structure using the following function, which converts the struct produced by define-datatype into a vector displaying all of its components.

(define structure-of
       (lambda (exp)
         (cond [(pair? exp) (map structure-of exp)]
               [(not (struct? exp)) exp]
               [else
                (list->vector (map structure-of (vector->list (struct->vector exp))))])))

Example:

> (define exp1 (parse-expression '(lambda (x) x)))
> exp1
#<struct:lambda-exp>
> (structure-of exp1)
#3(struct:lambda-exp x #2(struct:var-exp x))

[Note: Notation such as #3(a b c) indicates a vector of length 3 containing the elements a, b and c. In some of the examples below the vectors omit the length following the hash character and print as #(x y z ... )].

Copy this code into your solution files to allow you to check the validity of your parsers.

Exercise 1

Play around with parse and unparse. You need not hand in anything for this exercise. However, you should play enough with parse and unparse that you understand them well. Can you predict what will happen if you try to parse the application of a function of 2? Try to make up other predict/test examples of your own. The idea here is for you to take the time and really understand this parsing process. Ask your friendly or instructor if you're unsure about any details here.


> (define g (parse-expression '(lambda (x) (f x))))
> (unparse-expression g)
(lambda (x) (f x))
> (structure-of g)
#3(struct:lambda-exp x #3(struct:app-exp #2(struct:var-exp f) #2(struct:var-exp x)))
> (unparse-expression (parse-expression '(lambda (x) (lambda (t) (t ((lambda (x) p) z))))))
(lambda (x) (lambda (t) (t ((lambda (x) p) z))))

Exercise 2

Here is an extension of the grammar used in this section:


<exp> ::= <number>			lit-exp (datum)
        | <id>				var-exp (id)
	| (if <exp> <exp> <exp>)	if-exp (test-exp then-exp else-exp)
        | (lambda ({<id>}*) <exp>) 	lambda-exp (ids body)
        | (<exp> {<exp>}*)		app-exp (rator rands)

The extension makes the following changes to the earlier grammar.

It introduces a new type of expression, the if-exp
Lambda expressions may take multiple arguments; specifically the id field in the first grammer, which can only be a single identifier, becomes ids, representing a list of identifiers.
Accordingly, applications may also take multiple arguments; the rand field becomes rands, representing a list of operands.

Modify the datatype specification (i.e. the code in (define-datatype ...)) to implement this extension.

Write parse-2, a parser for this grammar.


> (structure-of (parse-2 '(lambda (x) (+ x 2))))
#(struct:lambda-exp
  (x)
  #(struct:app-exp #(struct:var-exp +) (#(struct:var-exp x) #(struct:lit-exp 2))))
> (structure-of (parse-2 '(if (happy? me) (smile me) (frown me))))
#(struct:if-exp
  #(struct:app-exp #(struct:var-exp happy?) (#(struct:var-exp me)))
  #(struct:app-exp #(struct:var-exp smile) (#(struct:var-exp me)))
  #(struct:app-exp #(struct:var-exp frown) (#(struct:var-exp me))))
> (structure-of (parse-2 '((lambda (x y z) (* x y (+ z 1))) 2 4 (expt 4 5))))
#(struct:app-exp
  #(struct:lambda-exp
    (x y z)
    #(struct:app-exp
      #(struct:var-exp *)
      (#(struct:var-exp x)
       #(struct:var-exp y)
       #(struct:app-exp #(struct:var-exp +) (#(struct:var-exp z) #(struct:lit-exp 1))))))
  (#(struct:lit-exp 2)
   #(struct:lit-exp 4)
   #(struct:app-exp #(struct:var-exp expt) (#(struct:lit-exp 4) #(struct:lit-exp 5)))))

Write unparse-2.

> (unparse-2 (parse-2 '(lambda (x) (+ x 2))))
(lambda (x) (+ x 2))
> (define g '((lambda (x y z) (* x y (+ z 1))) 2 4 (if (> 2 3) 17 (expt 4 5))))
> g
((lambda (x y z) (* x y (+ z 1))) 2 4 (if (> 2 3) 17 (expt 4 5)))
> (unparse-2 (parse-2 g))
((lambda (x y z) (* x y (+ z 1))) 2 4 (if (> 2 3) 17 (expt 4 5)))

It should be clear now that abstract syntax is not meant for human consumption. However, when writing a program that deals with syntax such as an interpreter, it is much easier to use a well thought out abstract syntax than to work directly with the concrete syntax.

rms@cs.oberlin.edu