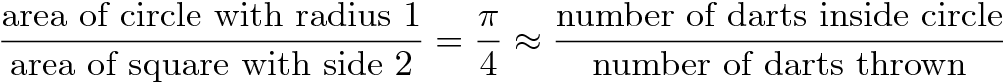CSCI 150: Lab 3

Visualizations
Due: 11:59 PM on Tuesday, March 2

The purpose of this lab is to:

  • Introduce basic graphics
  • Program your first visualizations!
  • Practice loops using graphics

Optional Prelab

In case it is helpful, we have put together a set of completely optional prelab questions (with an answer key) that might help you work through some of the ideas related to this lab before you start doing any programming. You can find these questions here in Prelab 3.

Part 1 - Picture This

sketchy.py: 10 points, individual

Implement a Design

 Create a program called sketchy.py that draws the picture of your design using the picture module.

Using the picture module

We have provided you with a module picture that lets you draw pictures. To use it you need to:

  1. As the first line in your program (underneath the header comments), add the line 

    
  import picture
  2. To get started, you need to declare and initialize a new picture object using a constructor function as follows: 

    
  canvas = picture.Picture(800, 600)
    This creates a new picture object called canvas which you'll be able to draw upon and display. The parameters are a pair of integers that specify the width and height of the canvas. Naturally, you can use other values if needed.

  3. At any given time, picture object keeps track of an outline color (lines and edges of shapes) and a fill color (the inside of shapes). The default values of these parameters are black and white, respectively. To change the color of the lines, you'd use the setOutlineColor function, as follows: 

    
  canvas.setOutlineColor(r, g, b)
    Here r is an expression indicating how much red the pen color should have (from 0 to 255). Similarly, g and b indicate how much green and blue are in the pen color. Some useful (r,g,b) values: (255, 255, 0) is yellow, (0, 0, 0) is black, and (0, 255, 255) is cyan.

    The function to set the fill color is what you might expect: 

    
  canvas.setFillColor(r, g, b)
  4. You'll also want to use the drawRect and drawRectFill function to draw rectangles and filled rectangles. For example, 

    
  canvas.drawRectFill(x, y, w, h)
    would draw a filled rectangle in the current pen color. The rectangle would be w pixels wide and h pixels tall. The upper left corner of the rectangle would be located at position (x,y). (Recall that the picture coordinate system, (0,0) is the upper left pixel.)

  5. As you may recall from class, the picture window will close as soon as your program ends, so if you want to be able to admire your creation, you'll need to force the program to wait. The easiest way to do this is by ending your program with an input statement: 

    
  input()

    Now when you run your program, it will open the picture window and keep it open until you press enter.
Here are a few of the additional things you can do:

  • setPenWidth(w) sets the pen and border width
  • setPosition(x,y) sets the pen position
  • setDirection(theta) and rotate(theta) changes the direction of the pen
  • drawForward(d) draws a line of the current color with current width in the current direction for the specified distance
  • drawCircle(x,y,r), drawCircleFill(x,y,r), drawRect(x,y,w,h), drawRectFill(x,y,w,h), etc. draw shapes, filled or not.
  • setFillColor(r,g,b) changes the fill color used when creating shapes
  • setOutlineColor(r,g,b) changes the color of shape edges and pen lines.

More details about these functions (and others!) can be found here. Please note that drawSquare and drawSquareFill might not be working.

Important Note

We would love to create an online art gallery sharing everyone's interesting art work. On this week's Google Form, please indicate whether your are willing to have your art work included in the gallery and whether you would like your work to be attributed to you (or to "Anonymous Student").

Part 2 - Walk Like an Egyptian

pyramid.py: 14 points, individual

Describe the Problem

 Write a program called pyramid.py that draws a pyramid of bricks based on user input.

Input: An integer for the width of the image (width) and the height in bricks of the pyramid (n).
Output: An image of a pyramid that is n bricks tall in a square canvas width wide (and thus width tall).

Understand the Problem

 Here are three sample outputs for your reference. Notice that the pyramid doesn't necessarily fill the entire canvas to the right and to the top; if the canvas width is not evenly divisible by the number of bricks, then there will be extra blank space. (A question for you to ponder: why is there so much blank space in the third example? Seems like you could fit lots of extra bricks both to the right and up top...)

400 x 400, 3 bricks.
3 bricks

400 x 400, 17 bricks.
17 bricks

400 x 400, 123 bricks.
123 bricks

Design an Algorithm

 Write pseudocode to draw the appropriate pyramid. The algorithm is:

  1. Prompt the user for the width width of the canvas.

  2. Prompt the user for the number of bricks tall to make the pyramid, n.

  3. Setup a canvas of size width by width with a cyan background.

  4. Start building the pyramid in the bottom left corner of the canvas. This is the tricky part so we will walk you through it. Very broadly, the algorithm to draw the actual pyramid is:
For each row i of the pyramid
  • Draw row i of the pyramid
Of course, this leaves a lot of details out! The first question you should answer is "How many rows are there in the pyramid?" The answer here is n (please ask if it is unclear why this is the case).

So we can rewrite the algorithm as:

For each row i from 0 to n-1 do
  • Draw row i of the pyramid
But drawing row i of the pyramid is a whole process in itself. To draw row i of the pyramid, we need to answer the following questions (which are also part of the optional prelab, where you can find the answer key):
  • How many bricks does the i-th row have (given that the 0-th row has n bricks and the (n-1)-st row has 1)? That is, numBricksi = ??? Write down your answer.
  • What is the side length s of each brick in terms of width and n? That is, s = ??? Write down your answer.
If we take another look at our pseudocode, it would look like this:

For each row i from 0 to n-1 do
  • Draw row i of the pyramid as follows
    • Draw numBricksi bricks, each with side length s
If we were to implement this pseudocode, we would see that all the rows would be squished up against the left-hand side of the canvas... that is, we haven't taken into account that each row itself starts a little bit further to the right than the row below it. Thus, our next questions (also from the prelab, which has an answer key):
  • What is the x-coordinate of the first brick of row i in terms of s and i (given that the 0-th row starts at x-coord 0)? That is, startX = ??? Write down your answer.
  • What is the y-coordinate of the first brick of row i in terms of s and i (given that the 0-th row starts at y-coord width - s)? That is, startY = ??? Write down your answer.
Now we have enough to complete our pseudocode with sufficient detail:

For each row i from 0 to n-1 do
  • Draw row i of the pyramid as follows
    • Draw numBricksi bricks, each with side length s
    • Each brick should have y-coordinate startY
    • The first brick should have x-coordinate startX and each subsequent brick should be offset by s from the previous

Implement a Design

 Now that you have a detailed algorithm in pseudocode, translate it (bit by bit!) into a Python program named pyramid.py. Although your final program should get the width and number of bricks from the user, you may want to temporarily hard-code this values into your program (using the example values above, perhaps) for now because it will make testing easier for now.

Remember you can use the notes at the top of this page to help you remember how to create a new canvas and draw rectangles on it using the picture module.

Implementation Notes
  • All the bricks you draw should be exactly the same size. While you can pass floats to various picture functions, including drawRectFill, in the end these values end up being rounded to integers (since all pixels have integer coordinates). To ensure your bricks are placed exactly as you intend, you may wish to do the rounding yourself.

  • On a related note, sometimes the brick size length won't divide evenly into the canvas size. In these cases, you will have gaps either to the right or to the top of the pyramid. This is okay. However, you should not have gaps to the left or on the bottom of the pyramid. Always start at the bottom left, putting the next brick right next to theprevious one and right on top of the previous layer.

Test the Program

 Try running the program with the examples given above as well as some others. Make sure you have gaps where you ought to, and that there aren't gaps where there shouldn't be any. Your pyramid should not be sloping to one side or floating in the middle. You shouldn't have some bricks that are larger than others. If it looks fishy, go back and examine your math equations, checking that the "integer division" is being used appropriately.

Don't forget to let the user input the width and number of bricks, if you were testing the program with hard-coded values.

Part 3 - Monte Carlo!

monte.py: 14 points, partner encouraged

If you choose to work with a partner, only one of you needs to submit a solution, but both of you should indicate your partner and who submitted a solution in your Google Form submission. You should also both read the Recurse Center's guide on pair programming before you begin.

You probably remember bumping into that peculiar number pi π = 3.14159265..., right? It comes up when you're talking about circles and trigonometry, but also appears in a bunch unexpected places that seem to have little to do with either. As a refresher, π can be defined as the ratio of a circle's circumference to its diameter. One interesting feature of π is that it's an irrational number, meaning it cannot be expressed as a fraction m/n where both m and n are integers; consequently, its decimal representation never ends or even repeats.

Since ancient times, mathematicians have been fascinated with the study of π and it's various properties. Early approximations of π, such as 22/7 and 355/113 were accurate to 3 and 7 digits repsectively (the latter approximation was the best known for nearly a millenium). Currently, more than the first trillion (a million million) digits are known. There are many ways to estimate π — for example, you could draw as precise a circle as you can manage, measure its circumference C and diameter d, and then divide C/d; this should give you π. Alternatively, there is a geometry-based approach due to Archimedes. We'll investigate a third approach using what is called a Monte Carlo method.

Monte Carlo Method

When we say we're using a Monte Carlo method, we usually mean we're going to do a bunch of random trials and observe the fraction of those trials that have a certain property. In our case, we're going to be throwing darts into a square region, and computing the fraction of those darts that land within a circle inscribed inside that square. Each throw is a trial, and the property we are concerned with is whether or not the dart landed inside the circle or not.

Describe the Problem:

 Write a program called monte.py that computes an approximate value of π.

Input: A number of trials n from the user.
Ouput: An approximation to π using a Monte Carlo method with n trials.

Understand the Problem:

 More precisely, we'll begin by (theoretically) constructing a target circle inscribed in a square. This is our dart board, and the target circle reaches all the way to the edge of the square. It might look something like the following:

π Target

Next, we'll simulate repeatedly throwing darts at random against the board above (we'll assume that our random throws alway hits the square, and are equally likely to land at any given point inside the square). We then look at the fraction of the darts that land within the circle out of all those that were thrown. I claim that if we then multiply this fraction by 4, we should have a good approximation to π. What sort of dark sorcery is this? Let's take a closer look.

The area of a square is the length of a side squared. Thus our square, with sides of length 2, has an area of 4. The area of a circle is π times the radius squared, so for a unit circle (with radius 1), the area is π. Therefore, the ratio of the area of our circle to the area of our square is precisely π/4. (That is, the circle takes up a π/4 portion of our dart board.)

Since each dart lands at a random location in the square, the probability that any one dart lands within the circle should be exactly the fraction of the square taken up by the circle: π/4. Thus, if we repeat this experiment over and over again, we'd expect roughly a π/4 fraction of the darts to land in the circle. By counting up the fraction that actually land in the circle in our experiments, we've gotten a probabilistic estimate for π/4, or a quarter of π. If we just multiply that estimate by 4, we've got our approximation for π itself. Restating our discussion as a formula, we have

That is, if you throw lots of darts and keep track of the fraction that land inside the circle, multiplying this fraction by 4 should give you an approximate value for π. Of course, it is only an approximation: suppose (by some cosmic fluke) that all the darts thrown land near the upper left corner, outside of the circle. Then your approximation for π would be 0 (a rather weak estimate). However, as the number of trials increases, the likelihood that your estimate is good increases as well.

A run of the program might appear as follows.

  % python3 monte.py

  This program calculates the value of π by
  simulating the throwing of darts onto a round
  target on a square background.

      How many darts to throw? 1
  The value of π after 1 iterations is 4.0

  


  % python3 monte.py

  This program calculates the value of π by
  simulating the throwing of darts onto a round
  target on a square background.

      How many darts to throw? 100
  The value of π after 100 iterations is 3.08

  


  % python3 monte.py

  This program calculates the value of π by
  simulating the throwing of darts onto a round
  target on a square background.

      How many darts to throw? 1000
  The value of π after 1000 iterations is 3.1

Design an Algorithm:

 Write pseudocode to approximate π via this dart-throwing method — you'll throw random darts at a 400-by-400 board, and calculate what fraction end up within the circle enclosed by that board. Try this on your own, and then confirm that your pseudocode looks something like the following:

  • Prompt the user for the number of darts n they want to throw.
  • Create a square picture with width and height = 400
  • Draw a blue circle inside the square (with a radius of 200 and a center of (200, 200)
  • Initialize a variable hits to 0. This variable keeps track of how many of the n darts actually land within the target circle.
  • for n iterations
    • throw a single random dart onto our board (drawn in the square picture)
    • if the dart lands within the circle, increment hits
  • Calculate the fraction of the n darts that landed within the target, that is, hits/n, and from this calculate the approximation to π as 4*hits/n.

Implement a Design:

 Translate your pseudocode into a Python program named monte.py.

In order to implement your pseudocode, you'll need to "throw a dart." Each dart's position is specified by an (x,y) coordinate, so to "throw" a dart, you just need to randomly generate two values for each dart throw (one for x and one for y).

Generating random numbers / Throwing random darts

Python has a module that will let you generate random numbers called random. To use it you need to:

  1. At the top of your program, add the line 
    import random
  2. You can get a random integer between 0 and 99 (inclusive) with the following call 
    rInt = random.randrange(100)    # returns an integer in [0,99]
    Another way to get the same result is with the following call: 
    rInt = random.randint(0,99)
  3. In order to generate a random integer between 0 and 399 (which you'll do for each of the x- and y-coordinates of each dart throw), do the following. 
    randX = random.randint(0, 399)  # randX is between 0 and 399
To display your dart throw, you can draw a small circle centered at your (randX, randY) point that you just randomly chose (please use a color that can be seen on top of the blue big circle).

Now that you have your dart throw, your next question should be: how do I know if I've hit the target? You'll do this by calculating the distance from the center of the circle to the dart and determining if it is within circle's radius and therefore inside the circle. The distance formula is given by:

distance formula

where for us, centerX = 200 and centerY = 200. So to find out how far a dart lands from the origin, we need a square root, which requires the math module.

Math module

You can gain access to the math module by including the statement: 
import math
at the beginning of your program. This will give you access to more advanced mathematical functions as well as a decent value of π for checking the correctness of your program later on. In particular, 
math.sqrt(exp)
will return the square root of the expression exp, and 
math.pi
is a constant representing the value of π. See the online documentation for more details, if you need them.
Now in your for loop, you can check whether the dart lands within the unit circle with the following block of code (called an if-statement):


 if dist < RADIUS:
    # the body of this if-statement will only be run
    # if the distance between (randX,randY) and the center of the circle is at most RADIUS
    # (that is, if your point (randX,randY) is inside the circle.)
    # So. What do you want to do when you hit the target?
As with the first program in this lab, you should add an input() statement so that the drawing of your Monte Carlo simulation remains up for the user to see.

Test the Program:

 Try running your program with an increasing number of trials. Ideally, the more trials you have, the closer to the real value of π you get. You should expect that each run produces a slightly different value due to the fact that it is using a random number generator.

Part 4 - Wrap Up

Congratulations! You have finished the third lab. As with every lab, your last job prior to submission is to complete a brief write-up by filling out a Google Form, which is also how you submit your Honor Code statement (so please do not forget to do this).

Handin

Finally, all you need to do is submit your solution to the assignment. To do so, please click on the "Submit" button in the top right of your programming environment. This will save all of your programs for myself and the graders to look at. You are welcome and encouraged to submit partial solutions to your assignment -- you can always resubmit by pushing the "Resubmit" button in the top right, which will save the latest version of your programs. We will only grade the latest version that you submitted. By submitting multiple times, you avoid accidentially forgetting to turn in any completed part of your assignment, especially in case you become busy around the lab due date.

A. Eck, A. Sharp, T. Wexler, M. Davis, and S. Zheng.